The tradition of writing a trilogy in five parts has a long and noble history, pioneered by the great Douglas Adams in the Hitchhiker’s Guide to the Galaxy. This post is no exception and follows from the previous four looking at a Neural Network that solves the XOR problem.
This time, I had a interest in checking out Google’s machine learning system, TensorFlow.
Last November, Google open sourced the machine learning library that it uses within their own products. There are two API’s; one for Python and one for C++. Naturally, it makes sense to see what TensorFlow would make of the same network that we previously looked at and compare both Python-based neural networks.
You can download the TensorFlow library and see some of the tutorials here.
It’s worth noting that TensorFlow requires a little mental agility to understand. Essentially. the first few lines of code set up the inputs, the network architecture, the cost function, and the method to use to train the network. Although these look like the same steps as the steps in Python or Octave, they don’t in fact do anything. This is because TensorFlow considers those to be the model to use, running them only within a session. This model is in the form of a directed graph. Don’t worry if that’s not too clear yet.
TensorFlow Code
To start with, we need to load in the TensorFlow library:
import tensorflow as tf
The next step is to set up placeholders to hold the input data. TensorFlow will automatically fill them with the data when we run the network. In our XOR problem, we have four different training examples and each example has two features. There are also four expected outputs, each with just one value (either a 0 or 1). In TensorFlow, this looks like this:
x_ = tf.placeholder(tf.float32, shape=[4,2], name="x-input") y_ = tf.placeholder(tf.float32, shape=[4,1], name="y-input")
I’ve set up the inputs to be floating point numbers rather than the more natural integers to avoid having to cast them to floating points when multiplying the weights later on. The shape parameter tells the placeholder what the dimensions are of data we’ll be passing in.
The next step is to set up the parameters for the network. These are called Variables in TensorFlow. Variables will be modified by TensorFlow during the training steps.
Theta1 = tf.Variable(tf.random_uniform([2,2], -1, 1), name="Theta1") Theta2 = tf.Variable(tf.random_uniform([2,1], -1, 1), name="Theta2")
For our Theta matrices, we want them initialized to random values between -1 and +1, so we use the built-in random_uniform function to do that.
In TensorFlow, we set up the bias nodes separately, but still as Variables. This let’s the algorithms modify the values of the bias node. This is mathematically equivalent to having a signal value of 1 and initial weights of 0 on the links from the bias nodes.
Bias1 = tf.Variable(tf.zeros([2]), name="Bias1") Bias2 = tf.Variable(tf.zeros([1]), name="Bias2")
Now we set up the model. This is pretty much the same as that outlined in the previous posts on Python and Octave:
A2 = tf.sigmoid(tf.matmul(x_, Theta1) + Bias1) Hypothesis = tf.sigmoid(tf.matmul(A2, Theta2) + Bias2)
Here, matmul is TensorFlow’s matrix multiplication function, and sigmoid naturally is the sigmoid calculation function.
As before, our cost function is the average over all the training examples:
cost = tf.reduce_mean(( (y_ * tf.log(Hypothesis)) +
((1 - y_) * tf.log(1.0 - Hypothesis)) ) * -1)
So far, that has been relatively straightforward. Let’s look at training the network.
TensorFlow ships with several different training algorithms, but for comparison purposes with our previous implementations, we’re going to use the gradient descent algorithm:
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
What this statement says is that we’re going to use GradientDescentOptimizer as our training algorithm, the learning rate (alpha from before) is going to be 0.01 and we want to minimize the cost function above. This means that we don’t have to implement our own algorithm as we did in the previous examples.
That’s all there is to setting up the network. Now we just have to go through a few initialization steps before running the examples through the network:
XOR_X = [[0,0],[0,1],[1,0],[1,1]] XOR_Y = [[0],[1],[1],[0]] init = tf.global_variables_initializer() sess = tf.Session() sess.run(init)
As I mentioned above, TensorFlow runs a model inside a session, which it uses to maintain the state of the variables as they are passed through the network we’ve set up. So the first step in that session is to initialise all the Variables from above. This step allocates values to the various Variables in accordance with how we set them up (i.e. random numbers for Theta and zeros for Bias).
The next step is to run some epochs:
for i in range(100000):
sess.run(train_step, feed_dict={x_: XOR_X, y_: XOR_Y})
Each time the training step is executed, the values in the dictionary feed_dict are loaded into the placeholders that we set up at the beginning. As the XOR problem is relatively simple, each epoch will contain the entire training set. To see what’s going on inside the loop, just print out the values of the Variables:
if i % 1000 == 0:
print('Epoch ', i)
print('Hypothesis ', sess.run(Hypothesis, feed_dict={x_: XOR_X, y_: XOR_Y}))
print('Theta1 ', sess.run(Theta1))
print('Bias1 ', sess.run(Bias1))
print('Theta2 ', sess.run(Theta2))
print('Bias2 ', sess.run(Bias2))
print('cost ', sess.run(cost, feed_dict={x_: XOR_X, y_: XOR_Y}))
That’s it. If you run this in Python, you’ll get something that looks like this after 99000 epochs:

As you can see in the display for the Hypothesis variable, the network has learned to output nearly correct values for the inputs.
The TensorFlow Graph
I mentioned above that the model was in the form of a directed graph. TensorFlow let’s us see what that graph looks like:
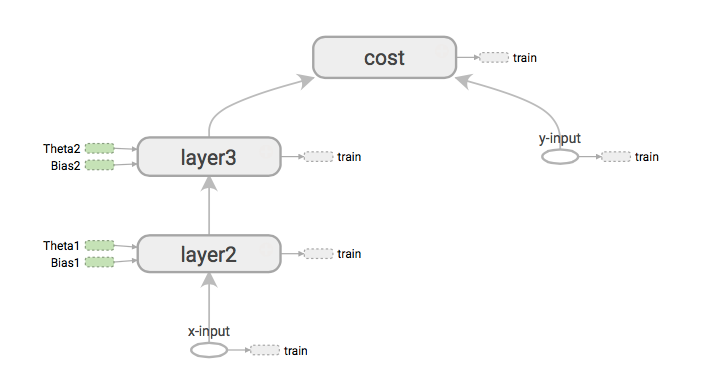
We can see that our inputs x-input and y-input are the starts of the graph, and that they flow through the processes at layer2 and layer3, ultimately being used in the cost function.
To see the graph yourself, TensorFlow includes a utility called TensorBoard. Inside your code, before the sess.run(init) statement add the following line:
writer = tf.summary.FileWriter("./logs/xor_logs", sess.graph_def)
The folder in the quotes can point to a folder on your machine where you want to store the output. Running TensorBoard is then as simple as entering this at a command prompt:
$ tensorboard --logdir=/path/to/your/log/file/folder
In your browser, enter http://localhost:6006 as the URL and then click on Graph tab. You will then see the full graph.
So that’s an example neural network in TensorFlow.
There is one thing I did notice in putting this together: it’s quite slow. In Octave, I was able to run 10,000 epochs in about 9.5 seconds. The Python/NumPy example was able to run in 5.8 seconds. The above TensorFlow example runs in about 28 seconds on my laptop.
TensorFlow is however built to run on GPUs and the model can be split across multiple machines. This would go some way to improving performance, but there is a way to go to make it comparable with existing libraries.
UPDATE 26/01/2016:
I’ve placed the full code up on GitHub here: https://github.com/StephenOman/TensorFlowExamples/tree/master/xor%20nn
Enjoy!
Update 07/03/2016:
I’ve changed the GitHub code to run a more realistic 100,000 epochs. Should converge now. [Thanks Konstantin!]
Hey, thanks for this tutorial!
I was implementing the XOR myself and somehow the NN won’t predict the correct values, when testing it. And I am running into the same problem, when using your code from GitHub…
At the end of the training process I am calculating the prediction accuracy which won’t get to 100% correct predictions, but stays at 50%. For this, I added these three line of code to the end of your solution:
correct_prediction = tf.equal(tf.round(Hypothesis), y_)
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(sess.run(accuracy, feed_dict={x_: XOR_X, y_: XOR_Y}))
And also when I output the Hypothesis’ values after training, all of them are somewhere close to 0.5, rather than 0, 1, 1, 0. I am outputting them with: print(sess.run(Hypothesis, feed_dict={x_:XOR_X})).
So is the XOR prediction actually working for you? Thanks!
LikeLike
Thanks for reading!
I suggest that there are a few things to check:
1. This algorithm really needs to run for about 100,000 epochs. I’ve noticed that my GitHub code only runs 5000, which is definitely not enough. I will update it.
2. Occasionally, the neural network gets stuck at a local minimum point in the solution space. Even after 100,000 epochs! So if you run the training again, the random starting values for Theta should sort that out.
3. You can also tweak the value of the learning rate, alpha, (the parameter to the GradientDescentOptimizer training function). This causes the steps in GDO to be bigger, lessening the chances of getting stuck in a local minimum. The downside of doing that is the risk of it not converging at all.
4. Lastly, you could use a different variant of gradient descent. That’s a job for another day though!
LikeLike
Hey, thanks for coming back to me! I could solve this issue by increasing the epoch size and/or decreasing the learning rate. Now works fine! 🙂
LikeLike
hi, I have a question: when I initialize Theta1 and Theta2 with tf.zeros() , it won’t work, why?
LikeLike
Hello Wei,
Think about what happens when all the weights are set to the same value. Every time the GradientDescent algorithm runs, all the weights are adjusted the same way. This prevents the network from actually searching through the solution space. To enable it to carry out this search, the algorithm needs to have random initial weights.
Hope this helps!
LikeLike
Why does my TensorFlow Neural Network for XOR only have an accuracy of around 0.5?
Wrote a Neural Network in TensorFlow for the XOR input. I have used 1 hidden layer with 2 units and softmax classification. The input is of the form , where:
> 1 is the bias
> x_1 and x_2 are either between 0 and 1 for all the combination {00, 01, 10, 11}.
> zero: is 1 if the output is zero
> one: is 1 if the output is one
The accuracy is always around 0.5. What has gone wrong? Is the architecture of the neural network wrong, or is there something with the code [ http://pastebin.com/qBawBnnZ ] ?
LikeLike
Hey there, thanks for the tutorial!
How would I go about giving the network a new input (I know that the training set included all possibilities, but just to test it) and feeding that through the network to see it get the answer?
Thanks
LikeLike
I believe the issue of why sometimes this code doesn’t reach convergence is because you are randomly initializing the weights using values in the range of -1 to 1 where as the initialization should be between 0 and 1. The cost function appears to be log loss which should be a convex function, but the initialization should be done with values in the appropriate domain.
LikeLike
Hello, thank you for this tutorial.
You can get better accuracy with a learning rate of 5 and only 10000 epochs. 4.5 second by changing the cost = tf.reduce_mean(tf.square(Hypothesis – y_))
LikeLike
Hey Luis have you changed the whole line of cost = tf.reduce_mean(( (y_ * tf.log(Hypothesis)) +
((1 – y_) * tf.log(1.0 – Hypothesis)) ) * -1) as tf.reduce_mean(tf.square(Hypothesis – y_)) ??
LikeLike
[…] Source : Solving XOR with a Neural Network in TensorFlow – On Machine Intelligence […]
LikeLike
after this training and all how can i plot a graph to show error vs epochs ?
Thank you !
LikeLike
Have a look at the matplotlib python library which is used a lot for generating plots.
LikeLike
Thank you for your response.. as you described that you have initialized the weights of theta 1 and theta 2 between -1 and 1. how can i see the exact initial weights of the input nodes and biases in this network ?
with regards.
LikeLike
Thanks for the tutorial, really helpful. I’ll also like to solve the XOR problem for complex valued neural networks(the inputs, weights, biases… are complex numbers). How do you suggest I got about this. Thanks
LikeLike
[…] Solving XOR with a Neural Network in TensorFlow […]
LikeLike